#6-2 정보검색 성능평가 (MAP, Pre@K, R-pre, NDCG)
by JiwonDev# MAP (Mean Average Precision)
용어가 나와서 어려워 보이지만, 사실 각 질의문의 평균정확률 (AP, Average Precision)을 더해 평균(Mean)을 낸 값이다.
AP(Average Precision) : 하나의 질의문(Q)에 얻은 검색문서에서 $ \frac{적합문서가 나온 곳의 Precision}{전체 적합문서의 수}$
앞 글 PRC에서 만든 표에서 (적합문서가 나온 정확률)만 뽑아내서 (전체 적합문서의 수)로 나눈다고 생각하면 된다.
2021.06.01 - [분류 전체보기] - #6-1 정보검색 성능 평가 (P, R, F1, PRC)
아래 표에서 적합문서의 위치는 Rank 1, 3, 6 이므로 각각의 정확률 (1.0, 0.67. 0.5) 를 더해서 나누면 된다.
이때 나누는 분모는 전체 문서가 아니라 '전체 적합문서 수'임을 유의하자.
AP = (1.0 + 0.67 + 0.5 ) / 5
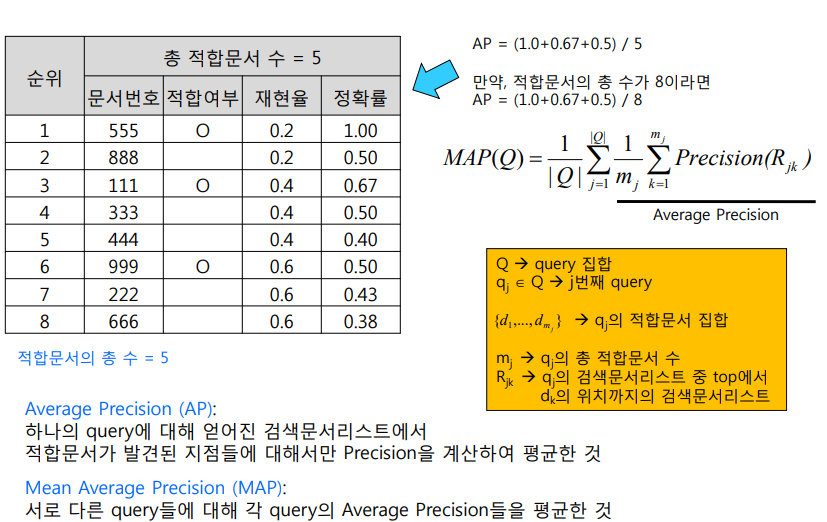
보통 모델을 평가할 때는 테스트용 질의문 50개 이상을 사용하니, 각각의 질의문에 대해 AP를 구해 평균을 내면 된다.
그게 바로 MAP(Mean Average Precision)이다.
위 예제에서는 질의문이 1개뿐이므로 그냥 AP를 구하면 그게 MAP이다.
# 예제
앞 글에서 푼 마지막 문제를 MAP로 풀면
Rank2 정확률(P) = 1/2(0.5)
Rank6 정확률(P) = 2/6(0.333) 이므로
AP = 0.5 + 0.333 / 4 (전체 적합 문서의 수) 이다.
질의문이 1개 밖에 없으므로 MAP의 값은 AP값과 같다.
3. 다음 표는 질의 Q에 대한 검색문서 집합 전체를 보인 것이다. 질의 Q의 적합문서집합 R = { 800:1, 690:3, 700:3 ,500:2 } 라고 할 때 아래 질문에 답하시오. ( 참고. 900:1 의미는 D900 문서의 적합도가 1이라는 의미이다. )
| Rank | Document No. | 적합도 |
| 1 | 381 | 0 |
| 2 | 800 | 1 |
| 3 | 456 | 0 |
| 4 | 451 | 0 |
| 5 | 761 | 0 |
| 6 | 690 | 3 |
| 7 | 295 | 0 |
# 상위문서 정확률 Pre@ (Precision at K)
그냥 앞에서 구한 표에서 특정 Rank의 정확률을 사용하는 방법이다. 진짜 말 그대로
Pre@3 = Rank3의 정확률 = 0.67
Pre@6 = Rank6의 정확률 = 0.5
정말 간단한 방법이다. 다른 방법과 다르게 총 적합문서의 개수를 알 필요도 없다.
다만 상위 Rank만 판단하다보니 앞부분에 나온 적합문서의 개수가 점수에 큰 영향을 미치므로 실제 점수를 구하는 좋은 방법이라고 볼 수는 없다. (=평가 성능이 불안정하다.)
이 방법은 웹 검색 모델을 평가할 때 자주 사용하는데 그 이유는 우리가 웹에서 검색할 때는 전체 검색 문서를 보지 않고 상위 10개정도만 읽으므로 (사람이니까) 전체 검색문서의 평균점수보다 상위문서 정확률이 더 중요하기 때문이다. 또한 웹 검색 결과의 경우 '적합문서의 개수'를 판별하는게 어려워서 다른 평가 방법을 쓰기도 까다롭기도 하다.

# R-precision
특정 질의문(Q)에 대한 (총 적합문서 수 == 문서집합 개수)인 정확률을 구한다.
이것도 간단하다. 아래 표에서 [총 적합문서의 수]는 5이므로 [문서 집합의 개수]가 5개가 되는 Rank5에서의 정확률(0.4)를 사용한다. 즉 적합문서 수에 해당하는 Rank를 참조하겠다는 말.
질의마다 해당 질의에 '적합한 문서의 개수' 는 다르다.
질의마다 [적합문서의 개수 == Rank] 지점의 정확률을 구해 다 더해서 평균을 내면 된다.

# NDCG (Normalized Discounted Cumulative Gain)
위에서 사용한 PRC, MAP, Pre@, R-Precision 의 경우는 이진 적합도(적합하다, 아니다)를 기준으로 분류했다.
그런데 실제 검색 모델에서는 다중 적합도(완전히 다름, 조금 비슷함, 많이 비슷함, 적합함)를 사용하는데, 이를 구현한 성능 평가 방법이 NDCG 이다.
NDCG의 수식은 좀 복잡한데, 아래 글을 읽으며 어떻게 이런 수식이 나오게 되었는지 이해하면 어렵지 않다.

NDCG는 CG에서부터 출발하였다.
# CG (누적이득, 누적사용자만족도, Cumulative Gain)
상위 K개의 검색문서에 대해서 단순하게 사용자의 만족도 값을 전부 더한 값이다.
만족도 값은 말 그대로 '사용자가 평가한 값' 이기 때문에, 단순히 더해주기만 하면 구할 수 있다.
(ex 3: 완벽함 2: 거의 비슷함 1: 약간 비슷함 0: 완전 다름)

당연히 이런 식으로 구한 CG(누적 만족도) 평가에서는 각 문서의 순위를 전혀 반영하지 못한다. 그냥 더했으니까
(제일 적합한 문서가 1순위든 6순위든 어디든 검색 결과에 있기만 했으면 CG값은 동일하다.)
# DCG (차감 CG, Discount Cumulative Gain)
Discount CG, 만족도 값을 단순히 더하지 않고, 순위에 따라 깎아서(Discount) 더하는 방법이다.
CG에서 일반적인 만족도를 사용했다면 DCG에서는 순위에 따라 점수를 깎는 식
단순한 예를 들어 $\frac{만족도}{문서개수}$ 의 값을 DCG 수식으로 이용한다고 생각해보자..
Rank1 = 점수/1 = 3/1
Rank2 = 점수/2 = 2/2
...Rank6 = 점수/6 = 2/6 이런 식으로 점수를 검색된 문서 수(==Rank 값)으로 나눠주면 된다.
다만 실제 검색 모델에서 패널티 값(Discount)은 이렇게 단순하게 계산하지는 않기에 수식이 좀 복잡해진다.

다만 DCG를 사용하여 순위에 따른 점수를 부여해도 '질의 마다 검색된 개수' 와 '적합 문서의 개수' 를 반영하지 못한다.
쉽게 말해 100개 찾아서 99개가 정답인 경우(99%), 3개 찾아서 3개다 정답인 경우(100%)에서 당연히 전자가 더 좋은 시스템인데, DCG를 사용하면 3개 다 정답 인게 더 점수가 높게 나온다.
이를 해결하기 위해 점수를 정규화(Normalized)한 NDCG를 사용한다.
#다시 돌아온 NDCG (Normalized DCG)
정말 간단하게 설명하면, 앞에서 구한 DCG 값을 IDCG로 나누어서 정규화 시킨 값이다.
IDCG(Ideal DCG)는 이상적인, 검색하면 적합문서만 나오는 100% 정확률을 가진 시스템에서 나오는 DCG값을 의미한다.

# 간단한 NDCG 예제
만족도 는 사람이 직접 평가한 값이며 ( 3: 완벽함 2: 거의 비슷함 1: 약간 비슷함 0: 완전 다름) 를 사용한다.
$CG_k$ 는 상위 K개의 문서에서 만족도의 합을 의미하며 만족도는 사람이 직접 평가한 값이다.
$DCG_k$ 는 $\frac{CG}{문서개수}$ 수식을 이용하겠다. CG와 마찬가지로 값을 다 더해서 구할 수 있다.
$IDCG_k$ 는 만족도가 높은 순으로 정렬되어 검색되는 완벽한 시스템에서 DCG 값이다.
아래 표에서는 Optimal Discount Gain (최적화된 DCG)라고 표기하였다.

그럼 계산방법은 간단하다.
$DCG_6$ = 모든 DCG의 합, 13.85
$IDCG_6$ = 이상적인 시스템에서 모든 DCG의합, 14.60
$NDCG_6$ = $\frac{13.85}{14.60}$
다만 위에서 말했지만, 실제 DCG 수식은 이렇게 단순하지 않기에 실제 NDCG는 아래의 수식을 사용한다.

물론 이를 사람이 직접 계산할 일은 없으므로, 우리는 $NDCG(Q,k)$ = $\frac{DCG_k}{IDCG_k}$ 만 기억하면 된다.
#퀴즈
3. 다음 표는 질의 Q에 대한 검색문서 집합 전체를 보인 것이다. 질의 Q의 적합문서집합 R={ 800:1, 690:3, 700:3 ,500:2 } 라고 할 때 아래 질문에 답하시오. ( 참고. 800:1 의미는 D800 문서의 적합도가 1이라는 의미이다. )
| Rank | Document No. | 적합도 |
| 1 | 381 | 0 |
| 2 | 800 | 1 |
| 3 | 456 | 0 |
| 4 | 451 | 0 |
| 5 | 761 | 0 |
| 6 | 690 | 3 |
| 7 | 295 | 0 |
3-1 MAP, Pre@5, R-precision을 구하시오
풀이
Pre@5는 Rank5에서의 정확률이므로
P = 1/5 이 정답이다.
R-precision 은 전체 적합문서의 개수를 Rank 위치로 생각한 정확률을 구하므로
전체적합문서의 개수 = 4개
Rank4의 정확률 P = 1/4 이 정답이다.
MAP 은 모든 질의문의 AP(평균정확률)을 구해 평균을 낸 값이다.
AP는 [적합문서가 나온 Rank의 정확률]의 합을 [전체 적합문서개수] 로 나누면 된다.
질의 Q에 대한 전체 적합문서 R={ D800, D690, D700, D500 } 라고 했으므로
Rank 2 => 정확률 1/2
Rank 6 => 정확률 2/6
질의 Q에 대한 전체 적합문서는 3개라고 했으니까
AP = (1/2) + (2/6) / 3
MAP(AP들의 평균)은 질의문이 1개밖에 없으니 AP의 값과 동일하다.
3-2 CG_7, DCG_7, NDCG_7을 구하시오. (단 Discount Gain은 Gain값을 순위로 나눈 값을 사용할 것)
풀이
CG는 단순히 검색된 문서에서 모든 만족도를 더한 값이다.
CG는 1+3 = 4
DCG의 값은 Gain 값(만족도)를 순위로 나눈 값을 사용 하라고 문제에 적혀있다.
즉 DCG = $\frac{만족도}{rank}$
DCG는 (1/2) + (3/6) = 1
IDCG는 모든 적합문서가 적합도가 높은 순서대로 나오는 완벽한 검색시스템에서의 DCG이므로
적합문서 R = { 800:1, 690:3, 700:3 ,500:2 }
IDCG = (3/1) + (3/2) + (2/3) + (1/4)
참고로 $ IDCG_7 $ 면 이런식으로 7번 더하면 된다. 다만 뒤의 값들은 0이라서 생략했을 뿐이다.
NDCG 는 $\frac{DCG_k}{IDCG_k}$ 이므로
NDCG = 1 / (3/1) + (3/2) + (2/3) + (1/4)
쉽다. IDCG를 구할 때 표에만 있는 적합문서가 아닌 '모든 적합문서'를 DCG 값을 구하는 것만 유의하자.
Precision, Recall, F1, PRC, MAP, Pre@K, R-precison, NDCG에 대해서 배워보았다. 총 8가지!
'🐱💻전공 공부 > 정보검색' 카테고리의 다른 글
| #8. 확률 모델(Probabilistic Model) (2) | 2021.06.01 |
|---|---|
| #7. 검색 성능평가 TestCase (0) | 2021.06.01 |
| #6-1 정보검색 성능 평가 (P, R, F1, PRC) (0) | 2021.06.01 |
| #5 벡터 모델 SMART 표기법 (0) | 2021.05.31 |
| 정보검색 #4 검색모델 (Retrieval Models) (0) | 2021.04.15 |
블로그의 정보
JiwonDev
JiwonDev