#6-1 정보검색 성능 평가 (P, R, F1, PRC)
by JiwonDev# 정보검색의 성능은 어떻게 평가할까?
1. Effectiveness, (효과성, 사용자 만족도)
정확률Precision(검색된 문서 중 적합문서의 비율), 재현율Recall(전체 적합 문서중 찾은 비율), F지표
2. Efficiency(효율성)
시간, 공간 복잡도 ( 문서당 평균 색인속도, 검색소요시간 )
-> 이는 알고리즘 성능의 영역이므로 이 글에서 다루지는 않는다.
# 그냥 정답을 맞춘 비율로 평가하면 되는거 아닌가요?
그걸 정확도(Accuracy)라고합니다.
이건 예를 한번 들어보면 왜 이게 구린지 알 수 있습니다. 환자 100명의 데이터가 있고, 그 중 5명의 환자가 악성 종양을 가지고 있다고 악성종양을 탐지하는 모델 A가 있다고 생각해봅시다.
모델 A : 아무런 동작없이 모든 환자 100명이 모두 정상이라고 판단, 100명중 95명은 진짜 정상인이고 5명은 틀렸으니 0.95(95%)
모델A가 정말 좋은 검색모델일까요? 당연히 아닙니다. 이렇게 데이터 자체가 한쪽으로 몰려있는 경우, 단순 계산한 정확도(Accuracy)는 믿을 수 없습니다.
# 정확률과 재현율 (Precision & Recall), F1 지표
정확률: 검색된 문서에서 적합 문서의 비율 $ = \frac{검색된 적합 문서 수}{검색된 문서 수}$
재현율 : 전체 적합 문서에서 찾아낸 적합 문서의 비율 $ = \frac{검색된 적합 문서 수}{적합 문서 수}$
전체 문서집합 {D1,D2,D3...D200}이 있고 200개의 문서중 질의 {Q}에 적합한 문서가 5개가 포함되어있다.
검색했을 때 6개의 문서가 검색되었고, 그 중 4개가 적합문서라면?
정확률 : $ = \frac{검색된적합문서수}{검색된문서수} = \frac{4}{6} = 0.6666\dots$
재현율: $ = \frac{검색된적합문서수}{적합문서수} = \frac{4}{5} = 0.8$

참고로 검색시스템마다 정확률, 재현율의 중요성이 달라진다.
예를 들어 특허/법률 분야의 검색에서는 전체 적합문서를 찾는 재현율을 높이는게 중요하며
일반적인 웹 검색에서는 나에게 적합한 문서만 보여주는 정확률을 높이는게 중요하다.
(일반 사용자들은 검색시스템이 가진 전체 적합문서가 필요하지 않다.)
정확률이 엄청 좋은데 재현율이 너무 낮은 시스템, 재현율이 뛰어나지만 정확률이 낮은 시스템
두 가지를 동시에 비교. 즉 (정확률+재현률)의 점수를 비교해서 검색모델을 평가 할 수는 없을까?
# F - Measure (F 지표)
실제로 이를 어떻게 할지 고민하다 나온 것이 조화평균을 사용하는 F지표이다.
조화평균이 뭐죠?
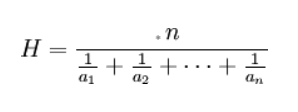
일반적으로 여러 수의 평균을 낼 때, 우리는 전부 덧셈하여 나누는 산술 평균(Arithmetic Mean)을 사용한다. 조화평균은 (주어진 수들의 역수)를 더하고 평균 낸 값의 역수를 취하는 방식이다.
이러한 조화평균은 음악의 화음(주파수의 역수)나 속도의 평균을 구할 때 사용된다.
같은 거리 S를 갈때는 10m/s, 올때는 20m/s 으로 왕복주행하였다면 평균속력은 단순한 산술평균으로 15m/s라고 생각할 수 있는데, 실제 시간과 거리를 계산해 속력을 측정해보면 대략 13.3m/s 정도의 속도가 나온다.
왜 결과가 다르게 나오나면 속력은 $ \frac{거리}{시간} $ 인데, 속력이 다르면 걸리는 시간도 달라지기 때문이다. 그래서 해당 공식을 시간에 대해서 아래와 같이 $ \frac{거리}{속력} $ 으로 구해야 쉽게 구할 수 있다.
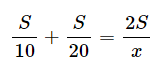
여기에서 x(평균 속력)에 대해 전개하면 위와 같은 조화평균 공식이 나오게 된다. 참고로 값이 2개 (a,b) 일때 조화평균(x)를 일반화하면 다음과 같은 계산하기 쉬운 공식을 얻을 수 있다.

정확률, 재현율은 분수로 이루어진 값이기에 조화평균을 사용해야한다.
여기에 필요에 따라 정확률(P)과 재현률(R)에 가중치 $ \alpha $를 둔 값이 F-지표이다.
다만 보통 2개의 값에 대해서 조화평균은 쉽게 구할 수 있는 공식을 사용한다.
$(a,b)$의 조화평균 공식 = $ \frac{2ab}{a+b} $
그래서 가중치를 이용해서 위 공식 모양으로 계산하게되면 위아래가 다음과 같은 모양으로 나오게 되는데 이때 계산된 가중치 값을 계산하기 편하게 $ \beta $ 로 치환했다.

참고로 계산해보면 알겠지만, $ \beta $ 값을 보고 가중치 $ \alpha $ 를 유추 할 수 있다.
$ \beta < 1$ 정확률(P)의 가중치 $ \alpha $ 가 더 높은 것이고
$ \beta > 1$ 이면 재현율(R)의 $ (1-\alpha) $ 가중치를 더 높게 준 것이다.
# F-1 지표
만약 여기에서 가중치 값을 둘 다 똑같이 50% (0.5)를 부여한다면 위 식에서 $ \beta $ 값은 1이 되어 다음과 같은 간단한 수식이 나오게 된다. 이를 $ F_1 Measure $라고 부른다.

자 이제 우리는 위의 복잡한 수식을 다 머리속에 지우고, 정확률과 재현률의 가중치를 50대 50으로 동일하게 준 $ F_1 $ 지표의 공식만 외우면 된다. 참고로 이는 (속력 a, 속력 b)의 조화평균 공식과 같다.
$F_1$ $Measure$ $= \frac{2 * P * R}{P + R}$
* 참고로 F의 의미는 그냥 이 지표를 발표한 학회(MUC-4, 1992)에서 이름지은거라 별 의미 없다. G(Geometry 평균 지표)와 함께 설명하면서 그냥 H는 이미 다른 곳에서 사용하고있으니 F라고 지은 듯하다.
# 정확률과 재현율의 한계
적합문서의 개수가 10개인 질의 Q에 대하여 적합문서가 { D0 } 하나일 때
System A : 5개의 문서 검색 $ \{(rank_1:D_4), (rank_2: D_3), (rank_3: D_1), (rank_4:D_2), (rank_5:D_0)\} $
System B : 5개의 문서 검색 $ \{(rank_1: D_0), (rank_2: D_1), (rank_3: D_2), (rank_4:D_3), (rank_5:D_4)\} $
이 두 시스템의 정확률(Precision)과 재현율(Recall)을 각각 구하면
시스템 A $P = 1/5, R = 1/10$ 이다.
시스템 B $P = 1/5, R = 1/10$ 이다.
당연하 P와 R의 값이 같으니, 이 둘의 평균을 낸 $ F_1 $ 지표의 값도 동일하다.
하지만 단순히 생각해도 실제 성능은 적합문서를 Rank1으로 찾아낸 시스템 B가 더 우수한 검색시스템이라 볼 수 있다.
그렇다면 순위(Rank) 정보까지 고려해서 정보검색 시스템을 평가할려면 어떻게 해야할까?

# Ranking을 포함한 정보검색 성능평가
1. Precision-Recall Curve (PRC)
정확률(P)와 재현률(R)로 그래프를 그리는 방법. 보통 정확률을 세로(y)축으로 사용한다.
* 물론 단순히 P-R 그래프를 그리면 그래프의 모양이 톱니모양(sawtooth)라서 제대로 평가 할 수 없다.
총 적합문서가 5개가 있고, 질의문(Q)에 대하여 8개의 문서가 Rank1~8로 정렬되어 검색되었다고 가정하면 아래와 같은 표가 나온다.
$Rank_1$ 검색된 문서집합 $ \{555\}$ , $R:\frac{1}{5}$ $P:\frac{1}{1} $
$Rank_2$ 검색된 문서집합 $ \{555,888\}$ , $R:\frac{1}{5}$ $P:\frac{1}{2} $
$Rank_3$ 검색된 문서집합 $ \{555,888,111\}$ , $R:\frac{2}{5}$ $P:\frac{2}{3} $
$Rank_4$ 검색된 문서집합 $ \{555,888,111,333\}$ , $R:\frac{2}{5}$ $P:\frac{2}{4} $
... 이런식으로 검색된 문서를 Rank 순서대로 1개씩 늘리며 그래프를 그리는 방법이다. (검색된 총 문서 개수만큼 점이 찍힌다.)

이 그래프의 모양을 이용해서 Rank이 반영된 점수를 매기는 방법인데, 당연히 저런 톱니모양 그래프를 비교하기가 어려워서 그냥 사용하지는 않고 보간(보정, Interpolated)하여 사용한다.
2. Interpolated PRC (보간 PRC)
PRC의 그래프 모양을 톱니모양이 아닌, 완만한 모양으로 바꾸는 방법이다.
재현률(r) 한 지점을 정해서, 그 지점보다 재현률이 같거나 큰 점들 중 가장 큰 max 정확률 값을 찾는다.
예를 들어 $P(0.2)$는 재현률(R)이 $0.2$ 보다 같거나 큰 지점중 가장 큰 정확률 값을 의미한다.
아래 그래프에서는 재현률이 $ 0.2 $일 때 정확률이 $ 1.0 $으로 가장 크므로 $ P(0.2) = 1 $
이런식으로 계속 구해나가면 아래 그래프의 ● 점만 남게되고, 나머지는 없어지게 되어 그래프 모양이 완만한 반달모양으로 바뀐다.
$ P(0.2) = 1.0 $ , $ P(0.4) = 0.67 $ , $ P(0.6) = 0.5 $

모든 P(재현률) 에 대해 수십, 수백만개의 점을 찍어 보간정확률을 구할 수 도 있지만, 보통 $ (0, 0.1, 0.2 \dots 1.0) $ 10% 단위로 11개의 재현률을 구해 구해 완만한 그래프를 그린다. (Averaged 11-point P/R graph)
아래 빨간색 그래프에서는, 어떤 시스템이 더 좋은지 그래프의 넓이를 구해 한눈에 파악 할 수 있다. (초록 > 파랑)

* 보통 그래프의 점수를 아래 넓이로(AUC, Area Under the Curve) 구해서 이를 AUPRC라고 부르기도 한다.
# 근데 질의문마다 그래프가 다르게 나올건데, 어떤 질의문을 기준으로 해야할까?
보통 검색모델을 평가 할 때는 최소 30개, 보통 50개 이상의 테스트용 질의문$(Q_1\dots Q50)$을 가지고 평가한다.
그 각각의 질의문에 대해 $P(0.0, 0.1 \dots 1.0)$ 을 구하고 각 재현률마다 평균을 구해 사용한다.
예를 들어 $Q_1$ :: $P(0.0) = 0.1$ $Q_2$ :: $P(0.0) = 0.2$ ... $Q50$ :: $P(0.0) = 0.15$
이렇게 결과가 나왔다면 $P(0.0)$ 값의 평균으로 $P(0,0)$ 의 값을 결정한다.
# 예제를 통해 좀 더 알아보자
전체 적합문서의 수가 4개가 있고, 질의 문서에 대해 총 15개의 문서가 Ranking 되어 검색되었다고 생각해보자.
위에서 배운대로 표를 그려도 되지만, 사실 Interpolated PRC에서는 적합문서가 나올때만 정확률의 값이 바뀌므로 전부 구하지않고 적합문서의 Rank 지점에만 정확률을 구해줘도 된다.
P( 재현률 ) = 해당 재현률(R)보다 같거나 큰 지점에서 가장 큰 정확률(P)

$Rank_1$ ${ 1 }$ , 적합문서 1/4개 $ P(0.25) = 1 $
$Rank_2$ ${ 1,2 }$ 적합문서 2/4개 $ P(0.5) = 1 $
$Rank_4$ ${ 1,2,3,4 }$ 적합문서 3/4개 $ P(0.75) = 0.75 $
$Rank_15$ ${ 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 }$ 적합문서 4/4개 $ P(1) = 0.27 $
적합문서 4개의 Rank 지점에서 정확률을 모두 구했으니 사잇값으로 11개를 쉽게 계산 할 수 있다.
$P(0.0) = 1$ , $P(0.1) = 1$ , $P(0.2) = 1$
$P(0.3) = 1$ , $P(0.4) = 1$ , $P(0.5) = 1$
$P(0.6) = 1$ , $P(0.7) = 1$ , $P(0.8) = 0.75$
$P(0.9) = 0.75$ , $P(1.0) = 0.27$
한번 더 말하지만, 'P(재현률)이 같거나 큰 값' 중에서 가장 큰 정확률을 적으면 된다.
그래프말고 하나의 평균 값으로 나타내는 방법은 없을까?
=> 평균정확률 (Mean Average Precision, MAP)
글 내용이 너무 길어져 한번 끊고, 다음 글에 설명하도록 하겠습니다.
# 퀴즈
참고로 3번 문제는 다음 글에서 다른 평가 방법으로 한번 더 설명할거니 편하게 한번 풀어보면 된다.
1. 다음 표로 부터 Accuracy, Precision, Recall, F1을 구하시오
| Relevant | Non-relevant | |
| Retrieval | 7 | 13 |
| Not Retrieval | 58 | 922 |
풀이
영어로 적혀있어서 당황했겠지만, 의미만 잘 알고있으면 크게 어렵지 않다.
Relevant(관련된, 적합 문서), Retrieval(검색된, 질의문에 검색된 문서) 를 의미한다.
P(Precision, 정확률)은 검색된 문서 중 적합문서의 비율를 의미한다.
P =7/20
R(Recall, 재현율)은 전체 적합문서 중 검색된 적합 문서의 비율를 의미한다. 분모가 '전체 적합문서 수'임을 유의하자.
R = 7/58+7 = 7/65
F1 지표는 조화평균의 공식으로 구할 수 있다.
$F_1$ $= \frac{2 * P * R}{P + R}$
$ F_1 $ = 2 * P * R / P + R
$ F_1 $ = 2 * (7/20) * (7/65) / (7/20) + (7/65)
A(Accuracy 정확도) 는 단순히 정답을 맞춘 비율을 전체문서의 수로 나누면 된다.
(적합문서 7+ 검색안한 문서 922) / (전체 문서 7 + 13 + 58 + 922)
A = (7+922) / (7+13+58+922)
2. 적합문서의 총 개수가 14인 질의(Q)에 대해 20개의 문서가 검색되었으며, 검색된 문서 중 5개의 적합문서가 포함되어 있다. 질의 (Q)에 대한 Precision, Recall, F1을 구하시오
풀이
P = 5/20
R = 5/14
F1 = 2*P*R / P + R
F1 = 2 * (5/20) * (5/14) / (5/20) + (5/14)
3. 다음 표는 질의 Q에 대한 검색문서 집합 전체를 보인 것이다. 질의 Q의 적합문서집합 R =
{ 800:1, 690:3, 700:3 ,500:2 } 라고 할 때 아래 질문에 답하시오. ( 참고. 800:1 의미는 D900 문서의 적합도가 1이라는 의미이다. )
| Rank | Document No. | 적합도 |
| 1 | 381 | 0 |
| 2 | 800 | 1 |
| 3 | 456 | 0 |
| 4 | 451 | 0 |
| 5 | 761 | 0 |
| 6 | 690 | 3 |
| 7 | 295 | 0 |
3-1 Precision, Recall, F1을 구하시오
풀이
문제가 헷갈릴 수 있는데, 질의 Q의 검색 결과가 표에있는 7개가 나온 것이고, 전체 문서중 적합문서가 3개(D800, D690, D830) 라는 의미이다.
표를 보면 알 수 있지만 질의문 Q에 대해서 D800, D690 총 2개의 적합문서가 검색되었다.
P = 2/7
R = 2/3
F1 = 2 * (2/7) * (2/3) / (2/7) + (2/3)
3-2 11-point P/R Graph의 좌표를 구하시오.
풀이
최대 정확률만 구하면 되니까 전체 표를 다 그리지 말고 적합한 문서의 Rank만 보면 된다.
총 적합문서는 3개라고 했고, 질의(Q)에 대해 적합문서가 2개가 검색되었다.
Rank 2, 총 2개 중 적합문서 1개{ ㅁ, D800 }
Rank 6, 총 6개 중 적합문서 2개{ ㅁ, D800, ㅁ, ㅁ, ㅁ, D690 }
Rank2 기준 P= 1/2(0.5), R=1/4(0.25)
Rank6 기준 P= 2/6(0.333), R=2/4(0.5)
그래프 값은 P( 재현율 ) 에서 해당 재현율(R)보다 크거나 같은 값중 최대 정확도이므로
재현율(R) 0.0 ~ 0.25까지는 P 0.5가 최대값
재현율(R) 0.25초과 ~ 0.5 이하까지는 P 0.333이 최대값
재현율(R) 0.5초과하는 경우는 존재하지 않으므로 P 0 이라고 생각하면 된다.
P(0.0) ~ P(0.2) = 0.5
P(0.3) ~ P(0.5) = 0.333, 재현율이 같은 경우도 포함하는 것을 유의하자.
P(0.6) ~ P(1.0) = 0, 해당 재현율이 존재하지 않는다면 정확률(P)의 최댓값은 0이다.
'🐱💻전공 공부 > 정보검색' 카테고리의 다른 글
| #7. 검색 성능평가 TestCase (0) | 2021.06.01 |
|---|---|
| #6-2 정보검색 성능평가 (MAP, Pre@K, R-pre, NDCG) (0) | 2021.06.01 |
| #5 벡터 모델 SMART 표기법 (0) | 2021.05.31 |
| 정보검색 #4 검색모델 (Retrieval Models) (0) | 2021.04.15 |
| 정보검색 #3 색인(Indexing) (0) | 2021.04.15 |
블로그의 정보
JiwonDev
JiwonDev