#8. 확률 모델(Probabilistic Model)

# 여담

앞에서는 벡터 모델을 주로 설명했었다. 사실 단순히 생각해보면 TF-IDF 모델을 사용하는 벡터 모델이 훨씬 좋을 것 같지만 확률 모델도 굉장히 성능이 좋은 BM25 (Best Match 25, Okapi)라는 모델이 있다. 실제 IR 서비스를 제공하는 ElasticSearch에도 5.0부터 BM25 알고리즘을 기본으로 채택해서 사용중. 재밌는 건 벡터 모델과 달리 수학적으로 전부 증명하고 모델을 사용하기 시작한게 아니라 다른 딥러닝 모델 성능 실험하는 것처럼

'어 이유는 모르겠지만 성능 엄청 좋은데? (=블랙박스)' 하고 쓰면서 조금씩 성능을 증명하고 있는 모델.

 

자, 여담은 여기까지 하고 이제 BM25이 어떻게 만들어졌는지 알기 위해서 확률 모델을 공부해보자.

* 아래 수식에서 BM25 (앞부분) * (뒷부분) 에서 앞부분에 확률 검색모델의 개념(IDF) 요소가 들어가있고, 뒤에 TF요소는 성능이 좋아서 넣은 거긴 한데, 왜 이 수식이 성립하는지 수학적으로 증명되지는 않았다. 아무튼 성능은 좋다.

수식이 복잡하지만, 신기하게도 동작하는 과정을 보면 tf, log(tf)와 비슷하게 동작한다.

---

# 설명하기전에

확률검색모델의 가중치 수식에는 '확률' 정보가 보이지 않습니다.

아래의 설명은 확률검색모델이 어떻게 확률정보가 보이지 않는 수식을 사용할 수 있는가? 어떻게 그 수식이 유도되었는가? 를 설명합니다. 수식을 외울려고하지말고, 이게 무슨 과정인지 이해하도록 합시다. (문제는 완성된 간단한 수식을 외워서 풀면 됩니다.)

# 확률 검색 모델

사용자의 질의에 대한 적합확률의 역순으로 문서를 순위화하는 아이디어를 사용한 검색모델.

 

[질의문(Q)에 대해서 나온 문서 D가 적합문서일 확률]

질의문(Q)에 대해 1. 해당 문서(D)가 나온다음 2. 그 문서가 적합문서(R, rel) 인 확률이라는 의미로

$P(확률|조건)$ $=>$ $P(R | D)$   또는   $P(R | Q,D)$  라고 적는다.

이 2개의 값을 사용하면 확률 모델을 만들 수 있지 않을까? 에서 출발한 아이디어.

 

확률 모델의 기본 아이디어는 어떠한 문서 D를 뽑았을 때 적합문서일 확률(rel), 부적합 문서일 확률(non-rel)을 각각 구해서 $ P(rel | D) > P(non-rel | D) $ 인 문서를 찾아내면 된다. 이를 가중치로 사용하면 $ \frac{적합문서가 나올 확률}{부적합문서가 나올 확률}$ 이 되겠다.

 

근데 어떠한 문서 D를 뽑았을 때 적합문서일 확률 ( $P(R|D)$ ), 부적합문서일 확률($P(NR|D)$)을 어떻게 구하는건 쉽지않다. 그래서 우리는 베이즈 정리를 이용해서 식의 모양을 바꾼다.

 

베이즈정리

1. 조건부확률 공식 유도하기

사건 A, B와 그 사건이 일어날 확률 $P(A) P(B)$가 있다고 가정하자. (단, $P(B) > 0$)

사건 B가 일어 난 후 사건 A가 일어날 확률을 $P(A|B)$라고 쓰자 그러면

$P(A|B) = \frac{A,B가동시에 일어날 확률}{B가일어날 확률}$ 이렇게 나타낼 수 있고 이를 수식으로

$P(A|B) = \frac{P(A \cap B)}{P(B)}$ 라고 적을 수 있다.

 

마찬가지로 거꾸로 뒤집어 A가 일어난 후 B가 일어날 확률은

$P(B|A) = \frac{P(A \cap B)}{P(A)}$ 이다.

 

이 두 식을 이용하면 

$P(A \cap B)$ =  $P(A|B) * P(B)$ = $P(B|A) * P(A)$ 라는 식을 만들 수 있다.  

 

2. 독립사건의 정의

두 사건 A,B이 일어날 확률이 서로에게 전혀 영향끼치지않는, 독립사건이라고 한다면

$P(A \cap B)$ = $P(A) * P(B)$ 이다.

이는 두 사건이 아니라 A,B,C,D... 여러개가 있어도 마찬가지이다.

$P(A \cap B \cap C \cap D)$ = $P(A) * P(B) * P(C) * P(D)$ 

 

3. 분할

사건 A를 여러개로 분할 할 수 있습니다.

사건 A를 $A_1, A_2 ... A_n$ 개로 분할한다면 이런느낌. (당연히 서로 겹치지않게, 각각의 사건이 서로소를 유지하면서)

 

4. 베이즈 정리 (Bayes' Law)

베이즈 정리는 $P(B|A) = \frac{P(A \cap B)}{P(A)}$ 에서 분모 $P(A)$값을 유도하는 과정에서 출발한다.

 

$P(A \cap B)$ = $P(A) * P(B)$

이 식에서 사건 B를 $B_1, B_2 ... B_n$ 개로 분할 한다면 다음과 같이 적을 수 있다.

$A =$ $(A \cap B_1)$ $\cup$ $(A \cap B_2)$ $\dots \cup$ $(A \cap B_n)$

마찬가지로 여기에 각각의 확률을 구하면 아래와 같은 식이 만들어지고

$P(A) =$ $P(A \cap B_1)$ $\cup$ $P(A \cap B_2)$ $\dots \cup$ $P(A \cap B_n)$

 

사건 A가 일어 났을 때, B의 분할 중 하나인 B_j라는 사건이 같이 일어날 확률은 다음과 같다.

이 식의 핵심은, 사건 $A$가 일어났을 때 $B_j$가 일어날 확률 ($P(B_j|A)$)을 거꾸로 뒤집은

$B$가 일어났을 때의 확률들 ($P(A|B_1), P(A|B_2) \dots P(A|B_k) 들$)로 나타낼 수 있다는 것에 있다.

 

5. 베이즈 정리의 응용

베이즈 정리는 사전정보, 즉 '데이터 분석을 통해 어떠한 사건이 일어날 확률 값을 이미 알고 있을 때' 사용되며 이를 이용하여 [어떠한 사건 A 발생 이후 일어날 확률] $P(\theta | A)$ 를 구할 때 사용된다.

 

예를 들어 [내일 하루 주식이 오를 확률]을 $\theta$ 라고 가정하자 ($\theta$ 는 0.0~1.0 사이값)

빅데이터 분석을 통해 [주식이 오를 확률] $\theta$ 가 0.4일 확률이 50%, 0.5일 확률이 50%임을 찾아냈다면

$P(\theta = 0.4)$ = 0.5    $P(\theta = 0.6)$ = 0.5 으로 적을 수 있다.

 

여기에서 주가가 3일 연속으로 오를 확률을 A라고 가정해보자.

3일 연속으로 올랐으니 A는 [내일 하루 주식이 오를 확률]을 3번 곱하면 된다. $P(A)$ = $\theta^3$

위에서 빅데이터 분석을 통해 [주가가 오를 확률  $\theta$]가 0.6이 될 확률이 50%임을 알고있으니

사건 A가 발생 한 후, [주가가 오를 확률  $\theta$]가 0.6이 될 확률은 다음과 같이 구할 수 있다.

위에서 유도한 식을 그대로 적은 것 뿐이다. A= 0^3 (세타 세제곱)

즉 베이즈 정리는 가지고 있는 확률 정보를 응용해서 새로운 정보를 도출해내는 공식이라고 이해하면 된다.

 

아래 적합문서 확률에 베이즈 공식을 적용한 예

---

 

 

다만, 베이즈 정리를 이용하여 확률을 구하려면

질의에 대한 모든 적합 문서(R)에 대한 확률 데이터가 있어야 하고

적합문서일 확률(R), 문서가 검색될 확률(D) 이 서로 독립적인 확률이라고 가정해야한다.

<궁금한 친구를 위한 추가 설명 링크>

 

독립적인 확률은 가정한다 쳐도 모든 적합문서에 대한 정보는 어떻게 구하죠?

사람이 수작업으로 만든다.

현재의 검색시스템들은 자동 적합성 피드백을 사용하기도 하는데 과정은 생각보다 복잡하니 대충 알아보고 넘어가자. #10 글에 적합성피드백에 대한 내용을 추가로 설명하겠다. 

자동 적합성 피드백은 효과가 없을 것 같지만, 적용 했을 때 결과가 더 좋아진다는 논문이 많아서 사용된다.

 

 

P (RD)는 특정 질의(Q)에 대해 나온 문서가 나올 확률을 의미한다.

 

베이즈 공식을 적용한 모습. 첫번쨰 식의 모양을 바꾼 것 뿐이다.

다만 정보검색에서는 '몇번째 순위까지 위 식을 만족하는 문서인가?'를 찾을 필요가 없다.

그냥 점수를 매길 수 있는 가중치 공식만 있다면, 그 공식을 이용해서 상위문서 순위만 정하면 된다.

다시 말해서 위 공식에서 나온 $\frac{P(NR)}{P(R)}$은 굳이 사용하지 않아도 상관없다. (이 문서의 적합문서 확률, 부적합 문서 확률을 비교해서 적합확률이 높은 경계값을 찾을 필요가 없다는 말이다.)

 

결국 $\frac{P(D|R)}{P(D|NR)}$이 큰 값이 정확률 순위가 높다는 말이니까.

그래서 확률 검색모델의 가중치(정확도)는 $\frac{P(D|R)}{P(D|NR)}$ 만 사용한다.

이진독립모델은 바로 아래에 설명이 적혀있어요.

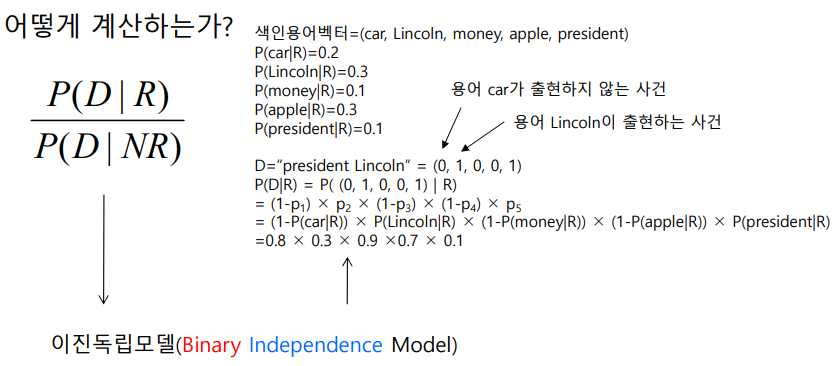
# 확률 검색모델의 모형

벡터공간 모델처럼, 확률 검색모델에서 용어의 적합여부는 여러가지 방법으로 계산 할 수 있다.

하지만 이 글에서는 간단하게 이진검색모델 (BIM)만 사용해보겠다.

이는 이름 그대로 용어의 출현 여부를 이진으로 구분, 즉 있다(1) 없다(0) 사용하고 문서 내 용어들의 확률은 서로 관련없는 독립적(Independence)인 확률이라고 가정한다. (베이즈 공식을 사용하기 위함)

단어들이 독립적이지 않는데 어떻게 이 모델이 동작하는지는 아직 정확하게 밝혀내지 않았답니다.. 그냥 써보니 성능이 좋길래 그렇다 치고 쓰는중

 

# 직접 구해보자

이를 수식으로 예쁘게 만들면 아래와 같다.

그냥 위에 식을 반으로 나눠 product로 계산하기 편하게 적은 것 뿐이다.

product 기호

제일 아래 수식은 {car, Lincoln ..} 이런 용어를 {1,2,3..} 으로 일반항으로 바꾸었을 때 나오는 수식.

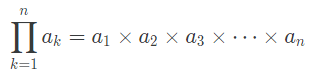
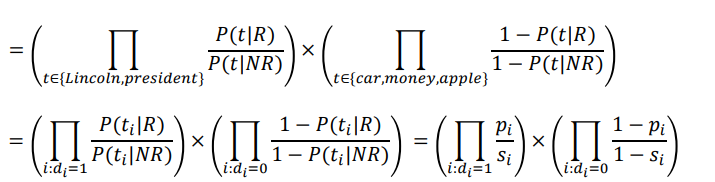
참고로 마지막에 $P_i$는 [i번째 용어가 적합문서에서 나올 확률],   $S_i$는 [i번째 용어가 부적합 문서에서 나올 확률]을 의미한다.

 

계산하기 편한 공식을 만드는 유도과정 (지져스..)

 

이 그림에서는 마지막 우측항이 '상수' 라서 버려도 상관없다는 것을 증명하는 내용.

수식을 유사한 값으로 바꿔 더 계산하기 편하게 변경. log를 사용하면 곱셈이 덧셈연산으로 바뀝니다. 이렇게 구한값을 RSV(검색 상태 값, 가중치)라고 부름

질의 Q에 대한 계산은 필요없다는 설명. 위에서 구한 RSV를 계산하는 방법

 

# 책 던지기 전에 예제부터 봅시다.

각 용어의 적합문서집합, 부적합문서집합에서 출현 정보가 있다면 계산이 엄청 간단해진다.

* 적합문서인데 (Relevant) 질의 내용(부산) 이 없는 문서도 있다는걸 유의하자. 

적합문서 집합 내에서 '부산'의 DF = 2,     부적합이면 전체(1000) - 2%

 

1. 출현 정보가 주어진다면 (↑그림)

부산이 적합문서에 있을 확률 $= \frac{부산이 출현한 적합문서}{전체적합문서}$,   $P_부 = \frac{r_부}{R}$

부산이 부적합문서에 있을 확률은 [전체 - 적합문서 개수]로 구할 수 있으므로

$= \frac{(부산이 출현한 모든문서)-(부산이 출현한 적합문서)}{(전체문서수)-(적합문서수)}$, 즉 아래 그림과 같다.

R = 적합문서일 확률, S = 부적합문서일 확률

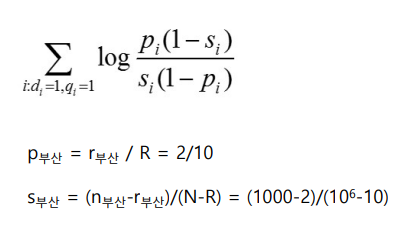
2. 만약 출현정보가 없다면

$P_i = \frac{1}{2}$,     $S_i = \frac{n_i}{N}$ 로 가정하고 구하면 된다.

$P_부 = \frac{1}{2}$,     $S_부 = \frac{n_부}{N}$ 으로 계산하면 된다.

 

 

3. 요약해서, 특정단어 i에 대해서

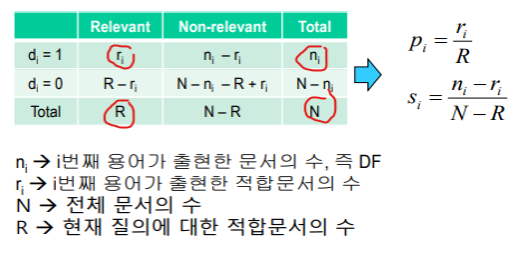
$\{ r_i, n_i , R, N \}$ 이 주어지면 적합확률($P_i$), 부적합확률($S_i$)을 구할 수 있다

$r_i$ = 적합문서에서 i가 출현한 문서의 수 (* i가 출현한 문서의 개수이다. 단어의 개수가 아니다.)

$n_i$ = 전체문서에서 i가 출현한 문서의 수

$R$ = 적합 문서의 개수

$N$ = 전체 문서의 개수

 

4. 실제 모델에서 사용하는 수식으로 적용한다면

유도과정이 복잡하지, 계산은 어렵지 않다. 아래 문제에도 나오니 한번 보고 가자.

- log를 이용해서 계산하기 편한 식으로 (유사값으로) 변경합니다. 로그는 곱셈연산을 덧셈으로 바꿔줍니다.

- log 0은 계산이 불가능하므로 분자, 분모에 0.5씩 더해줍니다.

이 공식을 그대로 적용해서 표를 그려보면 아래와 같습니다.

+0.5는 log 0을 방지하기 위해 넣은 값입니다.

 

---

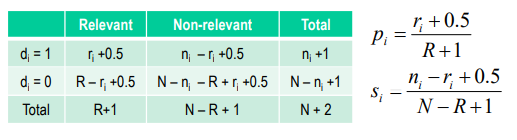
#BM25(Best Match 25)

위의 BIM(이진모델)의 최종 식의 유도과정을 보면 알겠지만, 문서의 출현횟수와 길이만을 이용해서 구했습니다.

즉 질의(Q), 즉 TF요소가 바뀌더라도 가중치에 영향을 주지 못합니다.

그래서 TF와 문서의 길이를 추가로 반영한게 BM25 모델이다.

문서(D)와 질의(Q)의 TF요소가 전혀 사용되지 않았다.

b는 미리 설정된 상수값이다. 보통 0.75정도 사용

그런데 문서(D)의 TF와 질의문(Q)의 TF는 어떻게 구했을까!?

어떻게 구했을까? 과연 어떤 수학천재가 유도과정을 통해 증명했을까!?

 

정답은 모른다. 그냥 가설을 세우고 느낌 좋은 값들 찍어넣었더니 성능이 좋아서 쓰고있다. 진짜로.

TF와 Length 값을 어떻게 찍어서 넣었을까요?

 

b는 미리 설정된 상수값이다. 보통 0.75정도 사용

상수 b의 값이 0이라고 생각했을 때

상수 k1, k2값을 적절히 조정하면 TF값에 따라 그래프가 linear (선형, 1:1), sub-linear(로그 그래프) 처럼 값이 매겨진다. 즉 벡터공간모델에서 사용했던 1+log tf 와 유사한 기능을 할 것이라고 추측해서 사용하니, 실제로 성능이 좋다고 한다. 물론 수학적으로 완벽하게 증명되지는 않았다.

 

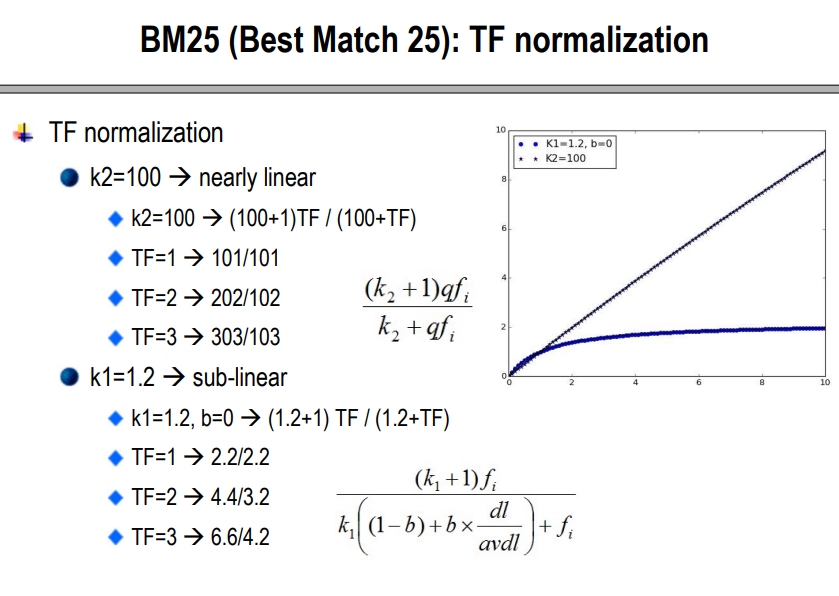
여기에서 상수 b는 문서 길이에 대한 가중치를 부여한건데

(평균적인 문서 길이와 비교해서, $\frac{문서길이}{평균문서길이]$) 문서길이가 클수록 가중치가 줄어들도록 만든 것이다. 이것도 벡터모델과 마찬가지로 tf*idf / n 와 유사한 동작을 한다고 볼 수 있겠다.

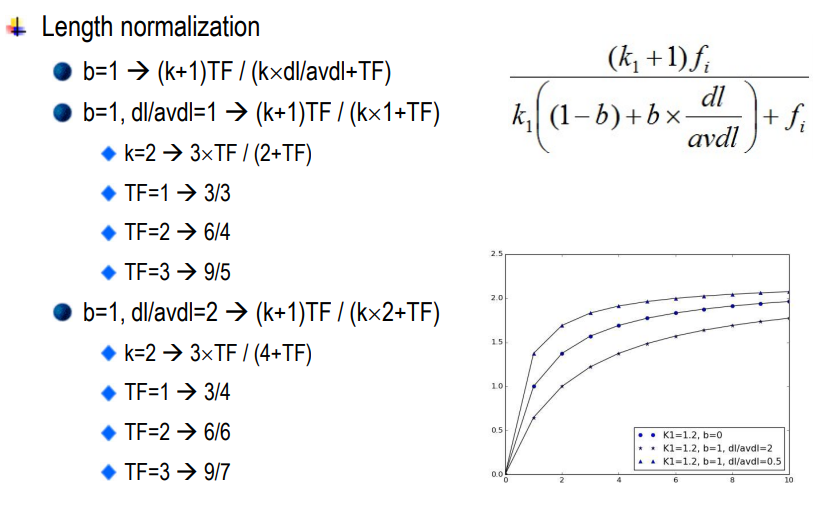
아, 물론 문서의 길이가 길다고 가중치가 낮아져야 한다는 보장이 있을까?
물론 반대로 생각하는 사람도 있다. 하지만 낮아진다는 가설을 사용하는게 성능이 더 좋아서 사용하는거 뿐이다.

 

결론

어찌보면 BM25의 식 3부분은 모든 질의용어에 대해서

$log idf * log tf(문서) * log tf(질의문)$ 의 값을 더한 수식이라고 생각할 수 있다.

거기에 tf(문서)에 길이에 대한 가중치값(dl/avdl)을 넣은 것. 

---

우리가 사용할 땐 해당 수식을 그냥 외워서 적으면 된다. (어차피 계산은 컴퓨터가 해주니까)

머신러닝 모델링 과정과 비슷하다. 이것저것 넣다보니 성능이 좋은 수식을 찾은 케이스.. 

<궁금한 친구를 위한 설명 링크> 를 여기쯤에서 한번 읽고 가자. 이해에 도움이 될거다.

 

 

---

# BM25 예제

이 예제에서도 알 수 있지만, 확률 모델이면 값이 0~1사이로 나와야하는데 이런 유도과정을 거치다 보니 전혀 상관없는 가중치가 나온다. 뭐 순위만 잘 비교하면 상관없긴 하지만.

---

---

# 퀴즈

다음은 전체 1000개의 문서로 구성된 문서집합의 일부와 질의 Q를 보인 것이다.

$Q =$ [한국, 대선]

$D2 =$ [한국, 한국, 대선, 미래, 선거]

$D3 =$ [민주당, 대선, 대통령, 선거]

df(한국)=100,   df(대선)=10,  df(미래)=20,  df(선거)=10,  df(민주당)=15,  df(대통령)=20

 

 

A. 아래 이진독립모델(BIM) 수식을 이용하여 Q와 D2의 유사도 및 Q와 D3의 유사도 계산 수식을 각각 적으시오.

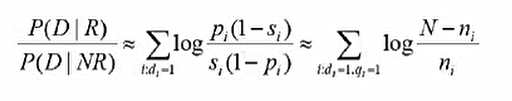
풀이

Sim(Q,D2)와 Sim(Q,D3)를 구하라는 문제. 공식은 묹제에 적어주었으니 그냥 풀면된다.

참고로 해당 수식은 적합/비적합 출현정보가 없을 경우 사용하는 확률모델 가중치 수식(=idf)이다.

 

Sim(Q,D2) 에서 Q와 D2에 공통으로 있는 단어는 {한국, 대선}이다.

한국, 대선에 대해서

$log \frac{N-n_한}{n_한}$

$log \frac{N-n_대}{n_대}$ 를 구한 다음 더해주면 된다.

 

$N$ : 전체 문서 개수

$n_한$ : 한국이 출현한 문서의 개수 ( df(한국) = 100 )

$n_대$ : 대선이 출현한 문서의 개수 ( df(대선) = 10 )

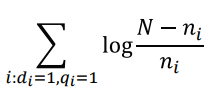
Sim(Q,D2) = $log\frac{1000-100}{100} + log\frac{100-10}{10}$

 

Sim(Q,D3) 에서 Q와 D3에서 공통으로 있는 단어는 { 대선 } 이다.

Sim(Q,D3) = $log\frac{100-10}{10}$

 

B. 질의 Q의 적합문서는 총 20개이며, 적합문서 집합 내에서 df(한국)=5,   df(대선)=7 이라고 할 때, 다음 수식을 사용하여 Q와 D2의 유사도 계산 수식을 적으시오.

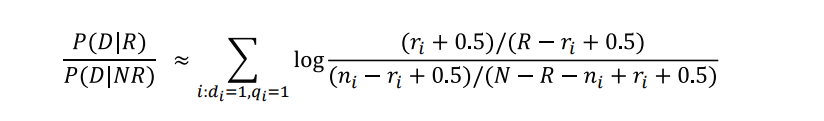
풀이

충분히 풀 수 있으니 한번 풀어보도록 하자.